Die Berechnung der Fibonacci-Zahlen ist eine wesentliche Herangehensweise zur Populationsbestimmung nach N Schritten. Relevant wird dies nicht nur bei Kaninchen, sondern auch bei Kettenmail-Angriffen zur Abschätzung des Email-Volumens nach N Empfängern.
Fibonacci ist wie folgt rekursiv definiert:
- a(1) = 1
- a(2) = 1
- a(n) = a(n-1) + a(n-2)
Eine Implementierung in einer Programmiersprache führt ab größeren N zu sehr langen Laufzeiten. Für N kleiner 34 kann eine 300MHz-CPU die Rekursion in unwesentlich weniger als einer Sekunde berechnen, N=35 benötigt bereits 1,5 Sekunden und N=40 knapp 30s.
Um die Fibonacci-Folge für größere N in erträglicher Zeit berechnen zu können gibt es den expliziten mathematischen Ansatz:
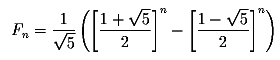
Diese Berechnung ist deutlich schneller, wie man im Ergebnis-Output sehen kann. Berechnet man die feststehenden Terme bereits im Vorfeld, so ergibt dies nochmal einen kleinen Geschwindigkeitsgewinn. Siehe FixedTerm-Math.
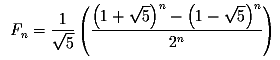
Obige optimierte mathematische Herangehensweise vermeidet die zweifache Division durch 2, indem sie 2 hoch n für den Nenner berechnet. Der Preis dieses Potenzierens ist allerdings niedriger als der der Division, so daß sich ebenfalls ein kleiner Geschwindigkeitsvorteil gegenüber der Standard-Mathematik-Methode ergibt.
Beide Methoden sind jedoch nicht exakt, da die Darstellung des irrationalen Wurzelausdruckes in endlichen Float-Typen nicht verlustfrei und somit ungenau ist.
Die direkte Iteration von 1 bis N-2 ist das schnellste Verfahren für mittelgroße N, für Größere benötigt auch diese Variante linear mehr Zeit, die mathematischen Herangehensweisen sind hingegen als zeitkonstant zu betrachten.
Die Ergebnisse
Hier die Resultate für eine Fibonacci-40-Berechnung auf einem AMD-K6-2-333:adi@drcomp:~/studium/inf/fibo$ fibo N for Fibonacci (i.e. 30) : 40 Will do Fibonacci for 40 Standard recursion for 40: Result: 102334155 Duration: 26.998583000s Mathematics for 40: Result: 102334233 Duration: 0.000006000s Optimized Maths for 40: Result: 102334233 Duration: 0.000004000s Fixed-term Maths for 40: Result: 102334233 Duration: 0.000003000s Iteration for 40: Result: 102334155 Duration: 0.000002000s
Gültigkeitsbemerkungen
Die hier gezeigten Ergebnisse sind alles andere als der Weisheit letzter Schluß. Weiterführende mathematische Verfahren wie die Verknüpfung von FixTerm- und Optimierungsmethode zeigen ein breites Feld an Varianten. Allerdings hat eben dieser Ansatz bei den Tests keinen weiteren Geschwindigkeitsvorteil gebracht.Des weiteren ist der Ergebnistyp Positive auf 32bit-Maschinen ein bißchen "eng", d.h., auch hier sollte man einen breiteren Datentyp verwenden, um mehr als 2 hoch 31 für den Folgenwert zu ermöglichen.